Why Put-Call Parity Is Such A Deep Insight
The essence of understanding that calls and puts are actually the same
Combining regular and masochist Money Angles in one today because the topic is covered calls.
I’ve crusaded against the “income” framing of selling covered calls or cash-secured puts. See:
The emphasis of these posts is the idea that without a view on volatility and honest performance attribution, there’s a good chance that you are confusing the high hit rate (cough, “cash flow”) that coincides with option-selling strategies and real economic edge.
[Think of dividends for a moment.
A dividend is cash flow but it’s not some extra edge. If the dividend wasn’t paid out, the cash would live on the companies books and you would be able to create your own dividend by selling the stock on your own schedule (in fact, stock prices fall by the amount of a dividend reflecting the fact that the company now has less assets). It’s just a re-shuffling of cap gains to dividend income. It’s more of an accounting/IRS thing and if it says anything about a company economically, it might be: “here take your earnings back we don’t think it’s a great time to re-invest them in our operations”.
I’m simplifying the multitude of reasons why a company might pay a dividend but if you really want the cynical take, it’s because some melting ice cube company is leveraging boomer-coded marketing around “cash flow” to finagle its way to a lower cost of capital. I’m shooting from the hip here, I couldn’t prove this, but the number of investing books in Barnes and Noble with “dividends” or “options for income” is suspiciously similar and I’m guessing corporate CFOs are capable of noticing what I notice. Reflexivity means the outputs become inputs. Bottoms up!]
Beyond the posts above, the real lift is to show investors that when they trade options, whether they know it or not, they are speculating on some weird abstraction called “volatility” not direction.
I’ve published the short version of that demonstration in The Beauty of Option Theory:
If directional trading is the most common use of options, then covered calls and hedging are the next most common. We can use a “replication mindset” to understand that even when you sell covered calls (or hedge) you are, regardless of how promoters sell the idea, engaging in a volatility trade.
Consider my logic:
The alternative to selling a 20d call monthly: you can sell 20% of your position instead.
a) Call selling: You get called away on your position about 1 in 5 months
b) Selling the stock: you are out of your position in 5 months
The false accounting that the call seller uses to rationalize: “I get called away on my position less than 20% of the time so actually selling the calls is better”
Reality: You are failing to account for the times when the stock dives where you don’t get assigned on your short calls, but you would have been better off to have sold 20% of your position.
The spread between the false accounting and reality is a function of the volatility that was realized vs the IV you sold
When you sell covered calls, whether it was a better choice than just selling the equivalent fraction of your position depends on what vol is realized vs what vol you sold.
If you sell calls too cheap you are better off just selling a fraction of your position and that’s why you shouldn’t sell calls indiscriminately for “income”. You need to consider whether the price is right.
Stop thinking of options through the lens of directional trading — you are still just trading volatility.
While I hope that conveys the point, I know there’s more appetite for a deeper explanation based on discussions with people who are earnestly trying to learn options.
This new post is a hands-on walk-through:
Covered Calls Are Still Just A Vol Trade (Moontower)
Some highlights:
- This homework will help a student understand why selling covered calls or cash-secured puts is not income. In fact, the student will see that options are always volatility trades — you will appreciate just how deeply insightful the concept of put-call parity is.
- I lean on a familiar setup: a binomial stock price process with discrete outcome. I use this approach in most of my technical posts because it conveys most of the intuition with simple arithmetic. If you can compute and average or combination formula in Excel, you are good to go.
The flow of the setup:
- Set up the tree of outcomes (we recycle the same framework from What We Can Learn From Vertical Spreads)
- Price the covered call we will sell and its delta. We don’t use a model. We can reason arithmetically about this.
- We practice computing P/L for various scenarios
- With computations now second nature, we can now get to the heart of the problem.

If you own a share of stock and it increases by $1, you enjoy a $1 profit and vice versa.
If you have a covered call strategy, and the stock increases by $1 you make $1 profit on your shares lose on your short calls. If you are short a 25% delta call, it will gain $.25 of value on that same $1 move.
Share position: +$1
Call position: -$.25
Net P/L: +$.75
- [If the shares go down in value you will lose $.75 (-$1 on the shares and +$.25 on the short call position.]
The key insight: at the inception of this portfolio you have a 75% exposure to the stock instead of 100%. You make or lose $.75 instead of $1 when the stock moves $1.
If you are a professional options trader explicitly playing the abstract game of “trading volatility” you’d hedge the entire delta…you would not want to have exposure to direction because you have no opinion on the company as an investment.
But the covered call seller clipping some coupon that “averages down their purchase price” or some marketing b.s. like that is now implicitly a volatility trader that just has a long bias.
The difference between this investor and the volatility trader is the investor is not going to continuously rebalance their share position to maintain a constant exposure to the stock.
[the other difference is the investor doesn’t realize they are now a “vol trader” but that’s the point of this whole post — to make this crystal clear]
The volatility trader tries to maintain zero exposure.
The covered call seller who sells a .25 delta call initiates a 75% exposure. However, the exposure is going to bounce around between 0 and 100% depending on how far the stock is from the strike price, how volatile the stock is, and how much time remains.
This is easy to understand at the extremes. If you are short the 103 call and long a share of stock trading for $200 you no longer have any marginal exposure to the price. If the stock goes to $199 or $201 you are unaffected. The owner of the call you are short is the one exposed to the stock. You can think of them as owning the shares that are in your account. Similarly, if the stock is trading for $10, you own 100% of the exposure. The 103 call you are short is worthless because it’s so far out-of-the-money.
We are ready to get our hands dirty again to explore the problem:
⚖️Portfolio Comparisons
Because the investor who sells covered calls is not explicitly “trading vol” they are not rebalancing. In our example, they are long the stock, short the .25 delta call, and just close their eyes until expiration.
This provides a perfect Socratic problem to work through to understand why the moment they traded an option they became vol traders.
Let’s continue.
You already computed the p/l for the covered call portfolio for every expiration scenario. The equivalent portfolio exposure that does not use options is to:
Simply sell 25% of your shares and hold the remaining 75%
This portfolio is initially equivalent to the covered call portfolio — it participates at 75% of the stock’s moves. And that will always be true. The covered call portfolio’s net exposure changes, as described earlier, but this is exactly why we can learn what it actually means to trade an option. This comparison will cut straight to the heart of options.
In sum, there are 2 portfolios:
A) Covered Call Portfolio consisting of:
- 1 long share from a price of $100
- 1 short 103-strike call at a price of $.69 (initially a .25 delta call)
B) Reduced Position Portfolio consisting of:
Long .75 of a share

We arrive at a milestone
If we compare selling a covered call to an alternative position where we just sell an equivalent delta worth of shares instead of selling a call, we see a very clear picture.
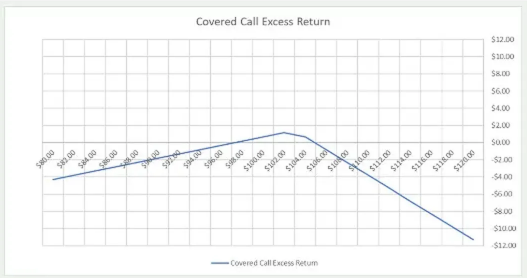
The covered call strategy is short volatility compared to the Reduced Position portfolio. It will outperform if the stock doesn’t make a large move and underperform if it does.
It simply doesn’t matter that you sold a call or a put or straddle or a strangle. If you sell an option, you are short volatility even if it’s a covered call or cash secured put.
The outcome of trading an option as opposed to just taking an equivalent option-free exposure will depend on what “volatility” you sold versus what volatility was experienced.
If you don’t have a view on volatility that differs from the market consensus (ie implied vol), the alternative portfolio where you trim your position by the delta of the option you would have sold, achieves the same exposure. (This is true over lots of trials which is how you should think about investing anyway).
The ensuing discussion allows us to internalize, generalize and relate the concepts to real-life investing decisions.
In our ongoing example, the option was sold at a fair price assuming the stock would move $1 per day. The remaining discussion will bootstrap your intuition for how the difference between implied volatility and realized volatility affects even a covered call portfolio held until expiration.
How volatility impacts your covered call option trade
We continue to assume you sold the 103-strike call at $.69, the fair value for the option if the stock moves $1 per day. It is rare that you trade an option at exactly the level of volatility the stock realizes until expiration.
Let’s look at the relative performance of the Covered Call vs Reduced Position for several scenarios. In each scenario we will examine:
- Excess return charts showing the p/l of the Covered Call Portfolio minus the Reduced Position, (ie 75% exposure portfolio) at each possible expiration price.
- The probability or “hit ratio” of how often the Covered Call Portfolio outperforms the Reduced Position exposure
- The expectancy of the Covered Call portfolio based on how much volatility the stock ends up experiencing
Remember, we expected the stock to move $1 per day which gave us a fair value of $.69 for the 103 call. Let’s see what happens when the realized volatility differs.
For example, what if the stock only moves $.90 per day?
https://notion.moontowermeta.com/lower-volatility-stock-moves-90-per-day
You’ll find plenty of pictures inside these scenarios:
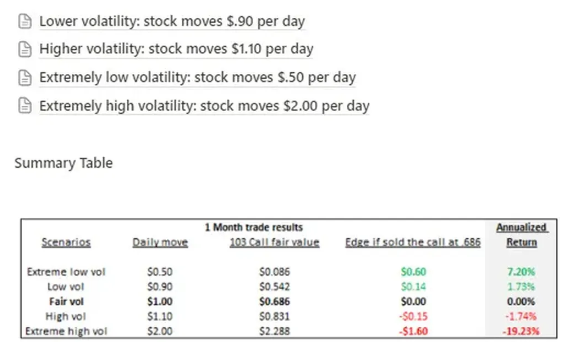
Things to note in the table:
- The skew in the results is what you expect if you decide to sell covered calls instead of just cutting your equity exposure…you are short an option.
- The justification for choosing to sell an option should demonstrate why it’s positive expected value to do so. This is not easy. You will experience a high win rate even when you sell the option too cheap (like in the “high vol” scenario). Even in the extremely high-vol scenario where you have made a disastrous trade you still win 1/3 of the time. The gap between win rate and expectancy is where the dragons of marketing and charlatans live.
- Options are not cheap to trade. Optically they may appear so but they are highly leveraged — study the table and you can intuit the relationship between those pennies and annualized return. The flip side of this shows why market-making is such a lucrative business. The fraction of a penny you don’t sweat is used to pay for private jets and political influence.
A concluding thought:
Put-call parity is not some dry academic idea. It is a profoundly deep insight. It does not matter which specific option expression you choose. The moment you opened an option account you committed to having a view on volatility. All the rhetoric around retail options trading is eliding the fact that the typical option user is poorly equipped to assess if volatility is cheap or expensive and without such a view should not be trading an instrument whose value depends on it.
The pitches all focus on the cadence of your returns…consistent income without confronting what really matters — is the option you are trading the right price? And without a view on volatility, you have no idea.
