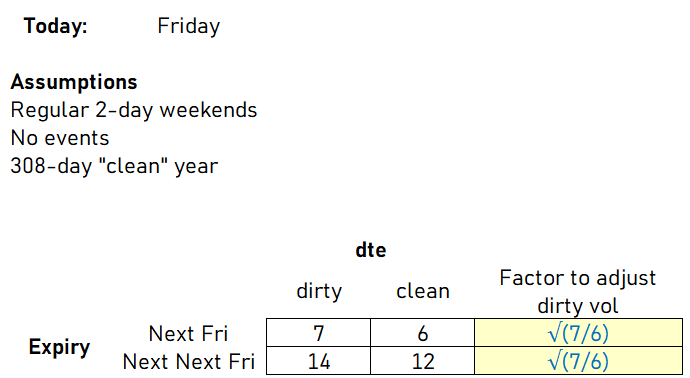two vol trader interview questions

Thursday’s post the dirties are down the cleans are up took the form of an extended interview question. If you are high-volume professional vol trader, the topic of vol time is fundamental but I don’t see much written about it. I hope my posts on it fill the gap.

For non-pros it probably best serves as a bicycle for the mind or a seed of inspiration but I wouldn’t stress over it. I suspect it does since tweets like this are popular even though I’m pretty sure the engagement on them isn’t coming from a bunch of practitioners in the middle of the trading day:

Most IVs you encounter use a 365-day model. To convert to a 251-day model (or any other tenor model) you multiply by the square root of the DTE ratio.

In the spirit of Thursday’s post and the tweet, I’ll pose 2 “interview-style” questions that can be answered in seconds. They require making a reasonable assumption. I’ll give the questions here, then I’ll post an assumption as a hint after the questions for those who need help forming one. The answers are at the end of the post. (Ignore cost of carry — also if you asked about that you’re way ahead of the game).

You do not need any calculators to answer these (just mental arithmetic).

❓#1: Volatility

It’s the close on Wed. Options expiring next Tuesday and next Friday have the same dirty vol (ie the same vol in your off-the-shelf 365d model). Does one of them have a higher clean vol? Explain. List any assumptions.

❓#2: Price of a straddle

It’s Friday close. Next Friday’s ATM straddle is $5. What price is the Friday ATM straddle expiring in 2 weeks to be the same clean vol? You do not need option calculator.

An assumption you could use to help:

We’ll use a calendar specification that states non-business days count as 50% of a business day for vacation time purposes.

If we continue to denominate our basic unit, a full trading day, as 1.0 and weekend days or holidays as .5 we get the following tenor:

251 x 1.0 + 114 * .5 = 308 day calendar.

Answers to the “interview” questions

#1: Tuesday has a higher clean vol than Friday.

Relative to a "dirty" year where each day is treated as equal vol, a "clean" year in which variances passes more slowly over a weekend, the Tuesday expiry has less time to expiry than Friday's ratio of clean to dirty DTE.

If the model implies the same dirty vol for Tuesday and Friday, we can infer Tuesday must have the higher clean vol bc it has relatively less vol time vis a vis a dirty model.

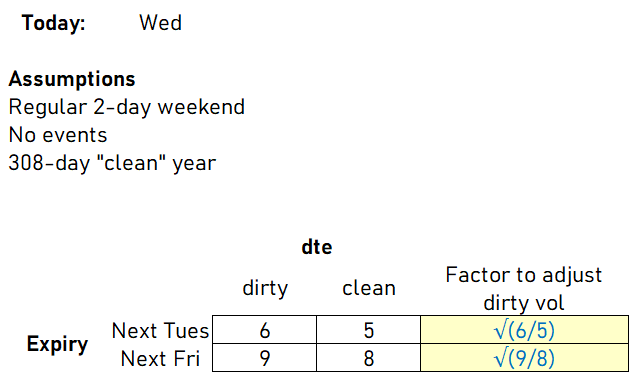
#2: The second Friday straddle must be $7.07

The approximation for an ATF straddle is .8*S*σ*√t

Since there is no cost of carry we can assume ATF straddle = ATM straddle which is what the question asks about.

We don't know S or σ but the question asserts the same dirty vol for both Fridays.

We know there's twice as much time to expiry for the 2nd Friday and we know the earlier Friday straddle is $5 so the second Friday straddle can be computed as

$5 * √2 since there's 2x as much time til expiry.

So the second Friday straddle = $7.07

💡This is one of those useful trader math ideas — for a given vol the price of the straddles only varies by square root of the ratio of DTE. One of those mental arithmetic things I found myself using constantly especially with short-dated options where you’re like “if the 1-week straddle is X, the 2 week is…”. This is also a clue to the degree to which I ditch the idea of “volatility” altogether in near-dated options and “think in straddles” and move sizes. This intuition is habitual but you can also see why it has theoretical support — vega p/l is a less of an influence on short-dated options. Results mostly come down to “how much did this thing move vs how it was priced”.

Returning to the question.

The $7.07 straddle is based on the same dirty vol.

But does that translate to the same clean vol the same as the first Friday straddle?

Yes — the ratio of dirty to clean DTE is the same for both expiries!