Probability Matching In Nature
A wild phenomena
Last week I used my twitter account in the name of science. I tried to replicate the results of a particular poll type I’ve seen recently.
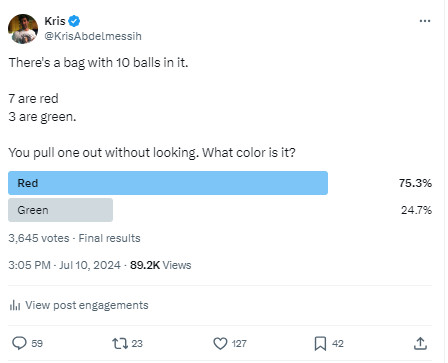
Seriously, wtf? Who picks green?
Why does the population response rate mirror the odds? In my poll, why doesn’t everyone choose red?
This is exactly what happens every time you ask a question like this. You spin a spinner that’s 60% blue and 40% green, what color will come up? And about 60% of the responses will say blue.
“Probability Matching”
This phenomenon has a name. Probability-matching. And it’s not unique to humans. Many species do this! Rats, birds, even fish [they set up a tank that feeds one side of the tank with X% probability and the other with (1-X)% and the population coalesces around the feeder in proportion to the odds].
In my poll, the reward-maximizing decision is to choose red. There is no dispute about that. So why does the optimal decision not express itself at the population level?
I’m going to point you to a video that is absolutely worth your time. Despite being a long (37 min), the presention by MIT finance economist Andrew Lo has fascinated so many people who’ve seen. It was totally captivating.
Shout out to @Jesse_Livermore for cutting the video to Twitter.
The video is totally worth it but if you don’t believe me I’ll share a few bits about probability-matching.
- From ChatGPT:
Definition
Probability matching is a decision-making strategy where the probability of choosing a particular option matches the probability of that option being the correct choice. Instead of always choosing the option with the highest probability of being correct (which is known as maximizing), individuals or algorithms using probability matching distribute their choices according to the observed probabilities.
Hypothesized explanations (these align with Lo’s angle)
a) Exploration vs. Exploitation Trade-off: Probability matching might be a strategy that balances the need to explore different options (to learn more about the environment) with the need to exploit known rewarding options. This can be beneficial in uncertain or changing environments where the best choice is not always obvious.
b) Evolutionary Adaptation: It could be an evolutionary adaptation that allows animals to cope with environments where resources are distributed in a probabilistic manner. By matching probabilities, animals might ensure a more consistent access to resources over time. - My thoughts from watching the video:
- Great demonstration of a fallacy of composition in the presence of high correlation (ie paradox of thrift is an unrelated example of a fallacy of composition. What’s optimal for individual <> optimal for the group)
- Lo says “nature abhors an undiversified bet”. I’m wary of evolution being personified as an agent. It feels that Lo’s conclusion is framed as nature being a portfolio constructor. I think it’s just the net result of arithmetic. The output is the same but my interpretation is a subtle tip-toe away from any connotation of nature having intent. I’m probably too dim to grok the particular nuances of Lo’s interpretation but the framing smells unnecessarily tidy to explain what could simply be the inevitable math of how a deck is dealt.
- In the last 2 minutes of the video, there is a remarkable observation about the simulation. If each individual’s behavior within the same generation is uncorrelated to the other individuals in the cohort then the optimal behavior is the self-maximizing decision since the generation’s aggregate “decision” will be diversified. It’s only in the presence of strong correlation that probability-matching is selected for.
- The parallels to portfolio construction are about as subtle as the sound of a piano falling off a balcony.
- The strategy may be a viable way to search the classic explore/exploit problem space. In my notes from Brian Christian’s interview, the explore/exploit puzzle is commonly referred to as the multi-arm bandit. And it’s as diabolical as a bandit:
In the multi-armed bandit problem you walk into a casino that has all these different slot machines. Some of them pay out with a higher probability than others, but you don’t know which are which. What strategy do you employ to try to make as much money in the casino as you can?
It’s going to necessarily involve some amount of exploration trying out different machines to see which ones appear to pay out more than others, and exploitation, which to a computer scientist doesn’t have the negative connotation that it has you know in regular English exploitation meaning, but just leveraging the information you’ve gained so far to crank away on those machines that do seem to be the best.
Intuitively I think most of us would recognize that you need to do some amount of both, but it’s not totally obvious what that balance should look like in practice, and indeed for much of the 20th century, this was considered not only an unsolved problem but an unsolvable problem, and sort of career suicide to think about. During WWII, the British mathematicians joked about dropping the multi armed bandit problem over Germany in the ultimate intellectual sabotage. Just waste the brainpower and nerd snipe all of the German mathematicians. To the field’s own surprise, there came a series of breakthroughs on the multi-armed bandit problem through the second half of the 20th century.
The notes go on to non-technical discussion of solutions. This is a problem every one of us faces from choosing careers to picking where to get take-out from.
Get quanty
Probability matching and Kelly betting (7 min read)
Robert Andrew Martin
Robert is an option trader I met a couple years ago. He wrote this post that:
discusses a cognitive bias called probability matching, explaining how it is rational from a population perspective. We then make an analogy to the Kelly criterion, a betting strategy that finds widespread use in both gambling and finance…
In their 2011 paper The Origin of Behaviour, Brennan and Lo make the wonderful insight that while probability matching is suboptimal from an individual level, it may be rational from a population level.
To motivate this, we’ll move from coin flips to a more ecological example.
You are an arctic fox trying to decide whether or not to change your coat from brown to white for the winter. If you have the wrong coat colour, i.e you turn white but it doesn’t snow, or you stay brown and it does snow, you get eaten by predators (sorry, I don’t make the rules). If you have the correct coat colour you survive and reproduce. The probability of no snow in winter is 75%. What is your strategy?
The best strategy for an individual fox is to always stay brown as long as P(no snow)>0.5𝑃(no snow)>0.5.
But consider the population perspective: if every fox stayed brown, then it would only take one winter with snow for the entire fox population to be wiped out. So the optimal strategy at a population level cannot be for every fox to stay brown, even though that is optimal for an individual!
Hopefully, this example illustrates intuitively why probability matching is a plausible strategy at the population level. In the next section, we’ll explore this idea mathematically.
Finally, quant and author of Advanced Portfolio Management:
This whole exploration has given me a new perspective.
Thank your innumerate co-humans. They are probability-matching for the good of the species.

