Path, VIX, & Hit Rates vs Expectancy
ways to price VIX and what we can learn from it
The CBOE’s VIX index interpolates 30-day implied volatility based on options struck on the SPX index.
A VIX future settlement price is based on the prevailing VIX index at the future expiry date. It’s a bit of a confusing concept. A future that expires to a VIX index level that looks ahead 30 days.
There are ETFs and ETNs that reference VIX futures (VIXY, VXX). They also come in levered and inverse forms (UVXY, SVXY).
Despite the abstract nature of trading “a level of volatility”, these are popular products. There is 2-way interest in them. SPX returns are inversely correlated to implied volatility making long VIX positions a natural hedge. At the same time, the upward-sloping term structure of SPX implied volatility means implied volatility in the future trades at a premium to volatility today. Many traders will short VIX futures and ETFs to capture the downward drift they expect if the market remains calm as the futures will “roll down” to converge with spot VIX by expiration.
Quant finance geeks about these volatility term premiums. Term structures recognize that volatility is mean-reverting. Historically, SPX realized volatility bounces around 15% give or take a couple percent over long periods. Implied volatility typically trades at a risk premium. The premium also bounces around but 16% IV on a 15% realized vol (ie 1% premium) is in the right ballpark.
The averages mask the distribution. VIX is bounded by zero. It’s rare for it to get to about half its average. It’s rare to double but less rare than halving from 15%. But it’s even possible to triple or quadruple (Covid and Aug 5th 2024 for recent examples). It’s also more common for VIX to go to 12 than 18, at least in recent years.
This low-res farmers almanac description paints a picture of a lognormally distributed index. VIX futures will drift lower frequently but occasionally spike and sometimes those spikes are very high (and fast).
It’s natural for us to think in terms of averages. This habit persists despite witnessing price moves that would be impossible if normal curves were in charge (and despite the warnings from cranky Lebanese deadlifters). The nasty side effect of Gaussian-brain is when it creates the illusion that something is massively mispriced when prices are just properly reflecting a skewed or fat-tailed distribution.
In the 2 min read, The Benefit Of Betting Culture, you can see how the price of a futures-style bet vs an over-under style focuses your attention on the distinction between probability and expectancy. This is the heart of the matter. Investors confuse hit ratios with expectancy constantly.
I field emails and calls too often that are basically retail traders saying “I was doing great selling options for 6 months then I lost it all in month 7”. The reasons for these mini-blow-ups vary from oversizing because they’ve been winning to naive pricing but the universal mistake is in the epistemology.
Some traders are executing without understanding the nature of the proposition. It’s not that selling options is a mistake (there’s a price for everything). It’s that you shouldn’t be surprised by the shape of the payoff. Roughly speaking, if I sell a 10-delta option every month and I win 6 months in a row, I haven’t learned anything about whether my strategy has an edge. I should expect to win most of the time. That says nothing about the expectancy. The person is thinking in terms of 50/50 averages, ie win or lose. But the proposition if it’s fair is more like win $1 9 times and lose $9 one time. If you have an edge, then you either win more often for the same payouts or the payouts are not as far apart but the hit ratio is the same. But most retail traders don’t have large enough sample sizes to infer anything from such skewed results. The track record is nothing but a statistically underpowered study.
Unlike rolling dice or flipping coins, it’s hard to learn anything about the distribution of prices from direct experience. Historicals help but you only have to look at acute incidents in markets over the past 5 years alone to appreciate the challenge of calibrating what’s improbable.
But we can strengthen our conceptual understanding to hopefully be a little less blind to hit rate vs expectancy (or median vs mean) illusions. Option surfaces themselves are great teachers in this regard. In a deeper understanding of vertical spreads, we’ve seen how call and put spreads are a rich source of information about a distribution.
In the remainder of this discussion, we’ll get some mileage towards internalizing the difference between hit rate and expectancy from a non-technical discussion about the price of a VIX future.
Pricing a VIX future (via arbitrage)
If you are a professional trader who just heard me say “price a VIX future” and “non-technical” in the same sentence, you feel like you’re at a Houdini act…” How’s this mf gonna pull this off?”
[cracks knuckles, bends neck side-to-side, deep breath]
Ok, a little background for the uninitiated.
The VIX complex of futures, ETFs, vanilla options and VIX options is one of the more technical areas of options trading. There are arbitrage triangles between these things.
They’re not exactly clean though.
Replicating a variance swap also isn’t clean (not every strike exists and even for the ones that do transacting entire strips is not economical). Neither is dispersion. Neither is isolating forward vol.
But all of these things lend themselves to a fair value that can be F9’d in Excel if you ingest the real-time bid/asks for the building blocks. Every large vol desk has a group that computes a fair value for VIX futures that is derived from SPX options and VIX options. You can trade around that fair value by being better bid on the building blocks that are relatively cheap and vice versa. Manage the residual risks and over time you make money.
I’ve never worked out a model for VIX futures fair value myself as I’ve never traded the SPX complex. But we can still step through it conceptually.
Imagine you are short 100,000 shares of VXX at $16.
*VXX references VIX futures. Just to avoid computing position ratios let’s just pretend VXX and the VIX futures trade for the same price.
You are short 100,000 vega because your position vega by definition is “change in p/l per 1 point change in volatility”.
If vol (ie the VIX future) drops by 1 point, you will make $100,000.
Arbitrage pricing comes from replication. If I can construct a portfolio with a cash flow of 0 in every state of the world, then I have a risk free position (and if I get paid to hold that portfolio I have an arbitrage profit).
To offset my VIX futures risk, I must therefore buy 100,000 vega via SPX options.
[This is conceptual, so we are hand-waving important details like what strikes, expires, weights and managing the deltas.]
At this point we are vega-neutral. Long SPX options, short VXX.
What happens if vol suddenly doubles?
You’re going to make a lot of money.
Why?
Because you lose linearly on your VXX short (-$1.6mm or 16 vol points on 100k shares) but you win more on your SPX option longs.
The reason: you are long not just ATM options but OTM options too. OTM options pick up more vega has vol increases. It’s like being long “vol gamma” (it’s literally called volga). Remember how a long gamma position gets longer delta as a stock goes up and shorter delta as a stock goes down. Well, this is the same effect but for vega via vol.
💡See Finding Vol Convexity for a full explanation.
The fact that you make money because your are long “vol of vol” means you aren’t quite replicating the VIX future though. That’s a problem.
[There’s a cost to being long “vol of vol” so we can deduce that vol never changed and expiration arrives that this so-called hedged position would have lost. There has to be a flip-side to the fact that if vol makes a large move that portfolio wins.]
Conveniently there is an instrument that’s a pure expression of “vol of vol”. You guessed it — VIX options.
The conceptual algebra:
VIX future = SPX options - VIX options
In our example, you can short VIX future, buy SPX options, and then sell VIX options to neutralize this long volga exposure.
This identity is loaded with insight.
- If I’m long VIX futures and short SPX options, I’m synthetically shorting “vol of vol”.
- If I’m short VIX futures and long SPX option, I’m synthetically long “vol of vol”.
- If I’m short VIX futures and long VIX options, I’m short vol but long vol of vol which is similar to be being short SPX straddle but long strangles.
You can envision how looking at the VIX complex you can see which leg stands out as cheap or expensive relative to the others. Layer in implied correlation which relates index vols to single stock vols and suddenly you’re Neo in the matrix.
A day in the life of a vol arb desk is market-making all the flows with an axe. Based on the price of the various parameters like vol, skew, convexity, term structure and correlation you might be:
- Selling VXX
- Buying 1-month VIX calls
- Selling 1-month single stock OTM calls
- Buying weekly SPX calls
- Selling SPX 6-month straddles
- Buying 9-month single stock downside puts
Like a chess player chunking their position, you look at this and think:
“I’m short SPX call spreads and vol near-dated, long upside implied correlation near dated, long a 6 month/9month time spread with a dispersion kicker.
I’m long gamma, short vega, long tons of volga, paying theta”
[Note: the greeks will vary based on the ratio of position sizes. If you’re playing along at home you can try to map the positions to the first line of the summary. And for the greeks you can try to imagine what position sizes are required to make the sign of the greeks make sense]
You do this not because these positions are inherently right or line up with some macro view. You do this because the prices are “right”.
You take what the market gives you. Everyone who’s out there trading on their opinions is moving the price of these parameters around. You are agnostic. Pick up the edge, manage the risk.
All you care about is others having strong enough opinions to move prices around and that you can find contradictions in the matrix.
To quote the closing line in Pacino’s speech in Any Given Sunday:
“That’s football folks. That’s all it is.”
Pricing a VIX future (like an option)
The fact that a VIX instrument has a fair value in a similar manner to how an ETF has a NAV has always kept me away from it. Just like I wouldn’t trade an ETF if I didn’t know its premium/discount. If a box has a dozen donuts I don’t want to buy it for a price that implies a baker’s dozen. Negative edge.
That said, lots of people trade VIX products with a belief that they have an edge based on a relative value lens rather than an arbitrage framework. I’m guessing this leads them to selling VIX futures (which is probably the right side from the arbitrage perspective as well.)
[I’ve often thought that if I were to build a VIX or SPX suite in moontower.ai I’d want to “do it right” which is to use the arbitrage lens rather than extending the in-place moontower analytics to VIX as if it applied. I’ll leave it to you to decide if other platforms do it right or if they’re like children playing house pretending to be grown ups. By the way I have similar opinions about 0DTE. I’d use a totally different framework than the one we currently use in moontower.ai to deploy a 0DTE suite.]
Since a proper VIX complex treatment is prohibitively scarce for retail, it’s additive to think about another way to price VIX. I think it’s intuitive to consider VIX itself an option.
(Again, we’ll stay conceptual. Working out the details is out of scope for this post).
I got the idea for “vix as an option” while answering a reader who emailed me. I’ll share my response so as to not expose the question explicitly.
I wrote (this is edited and expanded):
How do you model option prices and even the underlying price itself if it’s a future that is trading for $1 that will likely expire at 0 but can surge to $10 sometime before that? It's basically a bubble pricing problem because all known bubbles start to have that distribution and even tech stocks themselves in 1999 were pure extrinsic values themselves. It’s also the distribution that governs the H/J nat gas futures spread.
First let’s discuss pricing an option on this asset. Like what’s a reasonable vol for the $10 call?
I understand your temptation to think strike vol is “what IV will be when it gets there” but this like saying life expectancy is 85 if you survive the first year of life. The option needs to balance the price of many states of the world not just the conditional case. In other words, it’s more like what is your life expectancy at conception.
[For the technical, non-metaphor version see the “local vol” discussion in Chapter 7: Skew Trading of Colin Bennett’s Trading Volatility. The book is a free pdf.]
Another approach might be bootstrapping a discrete model. For example, you could use the price of vertical spreads to compute the implied distribution. Then you can those probabilities as your p and then fit various levels of vol to the call options in various states to see which vols are reasonable. I'd guess you'd end up with something that made the market look pretty rational. Like that call option might have a 10% chance of being 200 vol contributing 20 vol points to its IV and the remaining vol points are some sumproduct of the non spike scenarios.
One thing that a bit hairy is implied probabilities are “terminal” probabilities.
It's easy to understand the distinction when you think of VIX. You have a 9m future that's trading 18 but will probably expire at 12 or 13. But if I told you it's 75% to touch 30 during its life how does that effect your intuition of value?
If you use VIX call spreads to assess the probability you miss this because they will assign very little probability to touching 30.
Instead you can use the deltas (delta x 2 is a useful guess for a one touch probability). The one-touch probability is much higher because it respects path.
That was the end of my response. But a skeleton for pricing VIX as an option is there.
Think of the lognormal distribution (bounded by zero, positive skew, fatter right tail). As you increase volatility, the distribution “squishes” to the left.
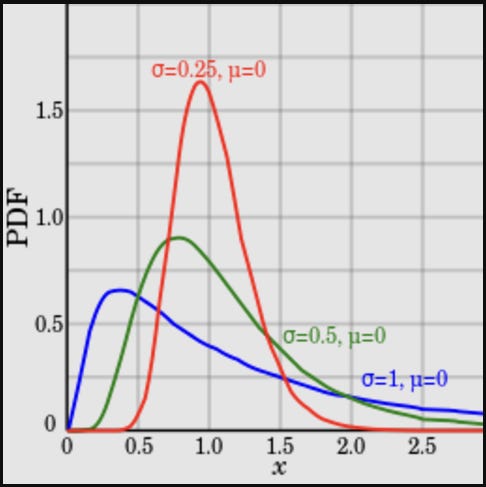
A look at March 2025 VIX Implied Distribution from the futures options
Here’s a condensed view of the Mar2025 options chain using mid-market for calls and puts.
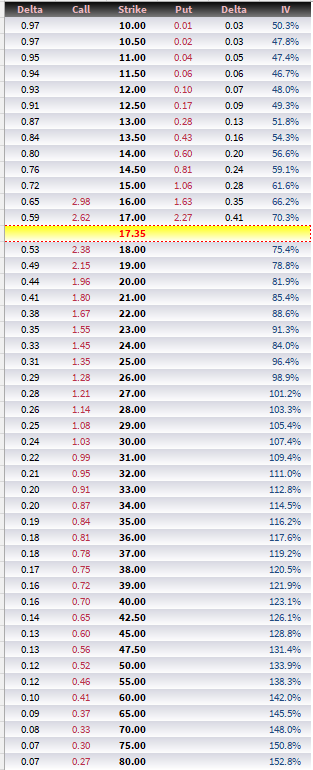
Things to note:
The extreme IV skew
- The 20% OTM call (~21 strike) is 3x the price of the 20% OTM put (~14 strike)
- The delta of that 21 call is 2x the delta of the 14 put
The distribution
Remember:
the price of a put [call] spread divided by the distance between the strikes estimates the probability that the underlying expires below [above] the midpoint of the strikes.
By looking at the spread of adjacent spreads (ie the butterfly) we estimate the probability density at the midpoint. If we do this across strike we have the implied PDF.
[It’s a bit noisy because of market widths and strike distances not being uniform but I normalized in a reasonable way for these artifacts]
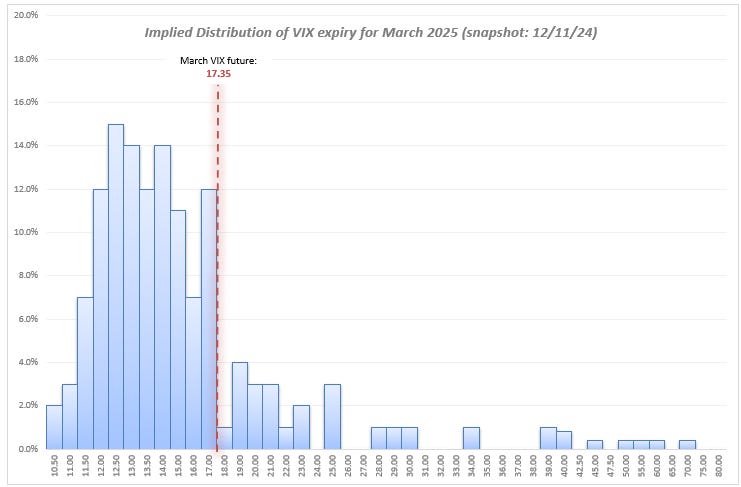
Even though the future is 17.35, the put spreads are expensive and the call spreads are very cheap telling us that March VIX is most likely to expire between 12 and 14.
If you are betting on roll down, it’s already priced in. The 16/14 put spread is $1.03 but the most it can be worth is $2. So despite the fact that the future is 17.35, you get slightly less than even money on the future expiring below 15. In other words, the future falling 14% is already baked in as the median outcome.
Implied distributions like this tell you the market expects the price to fall but it must still balance the chance that in the meantime it can double, triple, or more. It’s the kind of distribution you expect in bubble names where “the market can remain irrational longer than you can remain solvent” but everyone knows the asset is eventually going to be much lower.
Next time VIX spikes watch what happens. The VIX vols will pop, but the put skew will get smashed. The net effect is the put spreads get very expensive because VIX looks like a rubberband to investors…the higher it rips the more distance it has to snap back down which it eventually does. On a VIX rip everyone wants to buy put spreads to have a rick-contained way to capture that reversion, but the surface is too smart for that. You might end up with a VIX future at 25 and all spreads say…”meh, it’s going back to 15”. The contrarian bet would be to bet that it it’s NOT going back home. The options market will give you that bet all day. for good reason. But the trade you want to do is priced like a Chiefs point spread. Sure you’ll probably win, but the risk/reward a priori not a “excess return”. It’s consensus so you’re flipping coins for fair.
This is how the SLV surface repriced in 2021 when the WSB apes tried to squeeze it higher GME style. I was a very active silver options trader then and just found myself frustrated about how smart the surface was in adjusting. Speaking of GME, this type of extreme lognormal distribution took hold when Kitty roared. The cheap call spread beg you to buy them because nobody thinks GME is actually going to expire higher even though it might touch a high price. That it will touch a price is basked into the expensive calls outright and their deltas.
Look at the VIX chain again. The 30 call has a .24 delta. This implies that there’s a 48% chance that VIX will touch 30 at some point before expiry. With such a framework, you can start to see how the VIX future option vols and therefore deltas inform what the price of VIX futures should be. You might draw opinions about a VIX call being expensive relative to VIX itself (notice this is exactly equivalent to saying the implied volatility is expensive).
To be honest, this is all dancing around the fact that just pricing the VIX futures, SPX option, VIX option triangle is the final boss. But the point of this is to give you exercise in noticing that the fact that a VIX future is probably going from 18 to 13 doesn’t mean selling it is necessarily edge. There can be a better leg out there but focusing on “what will probably happen” is a form of probability myopia that distracts from expectancy thinking.
[The difference between positive expectancy and probability is the fertile soil of investing charlatanism. If you were to start a scam strategy from scratch you’d start with trades that have a high hit rate and just hope you collect enough profits before you see the whole distribution. Ideally with someone else’s money.]
We’ll leave it there.
Related reading:
