Option on Levered ETFs (part 1)
“They” say human labor will be irrelevant by 2027. By then, any business you can think will be solved by capital (electricity and tokens) before you brush your teeth in the morning.
You either get rich in the next year or join the permanent underclass.
So we aren’t shocked that the hottest fads in investing is pure return fuel:
- double, triple, even 5x levered ETFs
- options (record volumes, with nearly 2/3 of SPX options in 0DTEs!)
You’re not gonna break outta that underclass clipping 10% per year amirite?
I’m not here to judge whatever you think you need to do. The Moontower SOP, as always, is:

I give you tools, you use them as you see fit.
We need to talk about the collision of these trends:
options on levered ETFs
We can hack together a pricing framework. I say “hack” because we use a few building block concepts, combinations of arithmetic and logic, to construct a model. The process fuses several ideas I present often, reinforcing your comprehension of the basics, while alerting you to common misunderstandings.
We’ll do this in 2 parts.
Today, we cover four essential concepts:
1. Distance in return space
2. “Vol bonus”
3. Derivatives on derivatives
4. Option vega and convexity
Next week, we arrange the basics into a model for finding a fair price for an option on a levered ETF.
Essential Concepts
1) Distance
- A $100 stock that goes up 10% 2 consecutive days is now $121.
- A $100 stock that goes down 10% 2 consecutive days is $81.
In return space, $21 on the upside is the “equivalent distance” to $19 on the downside.
2) Vol “bonus”
I’ve written as much as can be written about vol drag/volatility “tax”/volatility “drain”, whatever you want to call it. It’s the “chop”. Up 10%, down 10% yields a cumulative return of -1%.
Trending leads to a vol “bonus”.
Imagine a 2x levered ETF on the $100 stock from earlier. Let’s say the ETF also starts at $100.
◾Reference stock goes up 10% 2 days in a row..
$100 —> $110 —> $121 or a 21% cumulative return
🟩2x levered ETF goes from $100 —> $120 —> $144 or a return of 44%
If you sized your ETF position half as large to have the equivalent risk or beta exposure you will have outperformed an equivalent risk holding over 2 days, although indifferent after just 1 day.
The vol bonus comes from trending.
If you step through a random walk where a stock can either go up or down X% you find that in most paths, the ones where we chop or recombine frequently (the paths fenced in red), your compounded return is less than if you simply added up all the daily returns and applied them to $100. Be careful: volatility doesn’t change your expectancy, only the distribution of return.
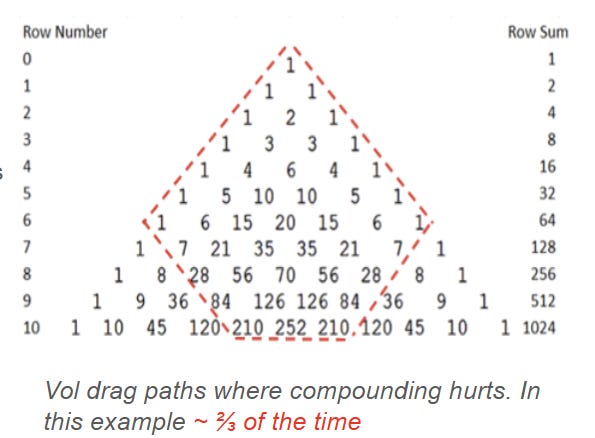
The infrequent, large vol bonuses offset the frequent vol taxes to keep the expectancy the same, even though you “usually” suffer a vol tax.
3) Derivatives on derivatives
A levered ETF is a derivative with a fair value. At any given moment, its NAV should be equal to:
NAV at the start of the day * (1 + reference asset’s return * leverage factor).
This is approximate since you should also deduct one day’s worth of expense ratio and the fund’s trading costs divided by the share count, however these values will have negligible impacts on daily fair value calcs for most users. The point is that a levered ETF is a derivative just like all ETF values are derived from an underlying basket, future, or security.
We want to price options on the levered ETFs which means we need a volatility surface. The reference asset’s option chain will provide a consensus vol surface. We pull a page straight from the arbitrage trader’s handbook — use a liquid market to price a closely related market after adjusting for the differences. This will provide a fair value of the levered ETFs options relative to the reference asset’s option prices.
4) Option values, vega, and curvature
We will cover one last “basic” before trying to reason our way towards a model for pricing options on levered ETFs.
Consider an at-the-money option.
💡Technically I should say at-the-forward but we can assume a RFR of 0% in which case ATM = ATF
If we double the vol, what happens to the option price?
It doubles.
The approximation for an ATF call:
ATF call ~ .4 * S * σ * √T
where:
S = stock price
σ = implied volatility annualized
T = fraction of a year until expiry
If c doubles, the call doubles. It has a linear dependence on vol.
💡Visual derivation of the ATF option approximation
Look at the approximation again.
What’s the vega of the ATF call?
Before you go searching for a Black-Scholes calculator, just recall that vega is the change in option value for a 1 point change in vol.
If σ increases by 1 point, the ATF call increases by .4 * S * √T
If we are pricing a 1-year ATF call on a $100 stock, if vol increases by 1 point, the ATF call goes up by $.40
Therefore, by definition:
ATF vega ~ .4 * S * √T
💡Example: Consider a 1-year ATF call on a $100 stock. If vol increases by 1 point, the ATF call goes up by $.40
Notice that the vega itself has no dependence on the volatility.
This is only true for ATF options!
Out-of-the-money option vega DOES depend on the vol level. It’s not hard to understand this intuitively.
Consider the 60 strike put on a 16% vol, $100 stock expiring in 3 months. 16 vol is roughly SP500 vol. The 3-month, 40% OTM put is probably worthless.
💡16% is a 1-year standard dev. 16%/√4 = 8% quarterly standard deviation. That put is 5-standard deviations OTM. Save me the Taleb-stanning that option is worthless.
A worthless option has no vega. If I raise the vol from 16% to 17% that put is still worthless. It has no sensitivity to the vol.
But that can’t be true for all levels of vol. If we 10x the vol to 160% then that put is now only 1/2 standard deviation OTM. It’s most definitely NOT worthless.
💡Re-framing volatility as time: Increasing the vol by a factor of 10 is algebraically equivalent to increasing time-to-expiry by √100. Even if we stick with 16% vol, a 40% OTM put on the SP500 with 100 years til expiry is clearly valuable
So we know that the 60 put acted like it had 0 vega when vol went from 16% to 17% but when vol 10x we expect the option to have a non-negligible valuation. Somewhere along the line, this option “picked up vega” or sensitivity to volatility.
While the ATF option is a purely linear dependence on implied vol, the OTM option’s dependence ranged from 0 to some positive number. This is the source of vol convexity.
A far OTM option might have no vega. But as implied vol increases, that option’s strike “becomes closer” to the ATM strike. I mean if vol is 200% there’s really very little difference between the 70 strike and the 60 strike in terms of standard deviation.
As vol increases, OTM option vega increases. If you keep jacking up the IV, the vega eventually peaks. The maximum vega an option can have is the ATF vega, which has no dependence on vol level at all.
I computed European-style option values using Black-Scholes for a range of strikes for 3-month options on a $100 stock using 20% vol at each strike.
Then I doubled the vol to 40% on each strike and computed the difference in option values:
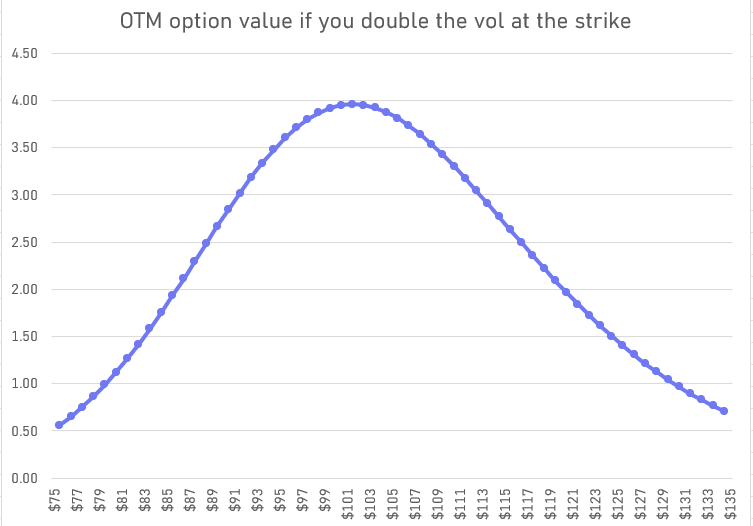
The ATM options have the most vega and will be the most sensitive to vol so naturally they go up the most.
But remember, at 20% vol some of those OTM options would be close to worthless but when vol doubles, an option like the 80 put went from $.04 to $1.16! On the chart, it gained $1.12.
If vol doubles instantly, your ROI on an ATM option is 100% but doubling the vol on an OTM option leads to comical ROIs:
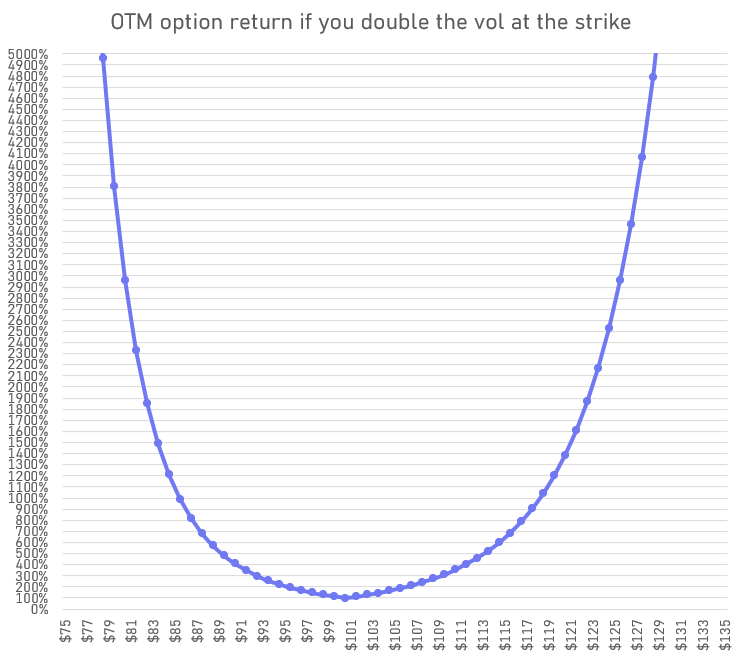
At the extremes, you get divide by zero errors as the return is infinite on a previously worthless option.
💡Clarification: I’m measuring changes in the OTM option on each strike. In other words, the “extrinsic” option. So for the 90 strike we are using the put, but the 110 strike, the call. The price changes will be the same for the call or put on the same strike, but the ROI due to a vol change shouldn’t be muddied by the instrinsic value which is constant on our examples, so we use the OTM option.
We’ve covered the essentials, next week we’ll answer:
- How do we translate the reference asset’s vol surface to the levered ETF?
- What does this mean for strike selection?
