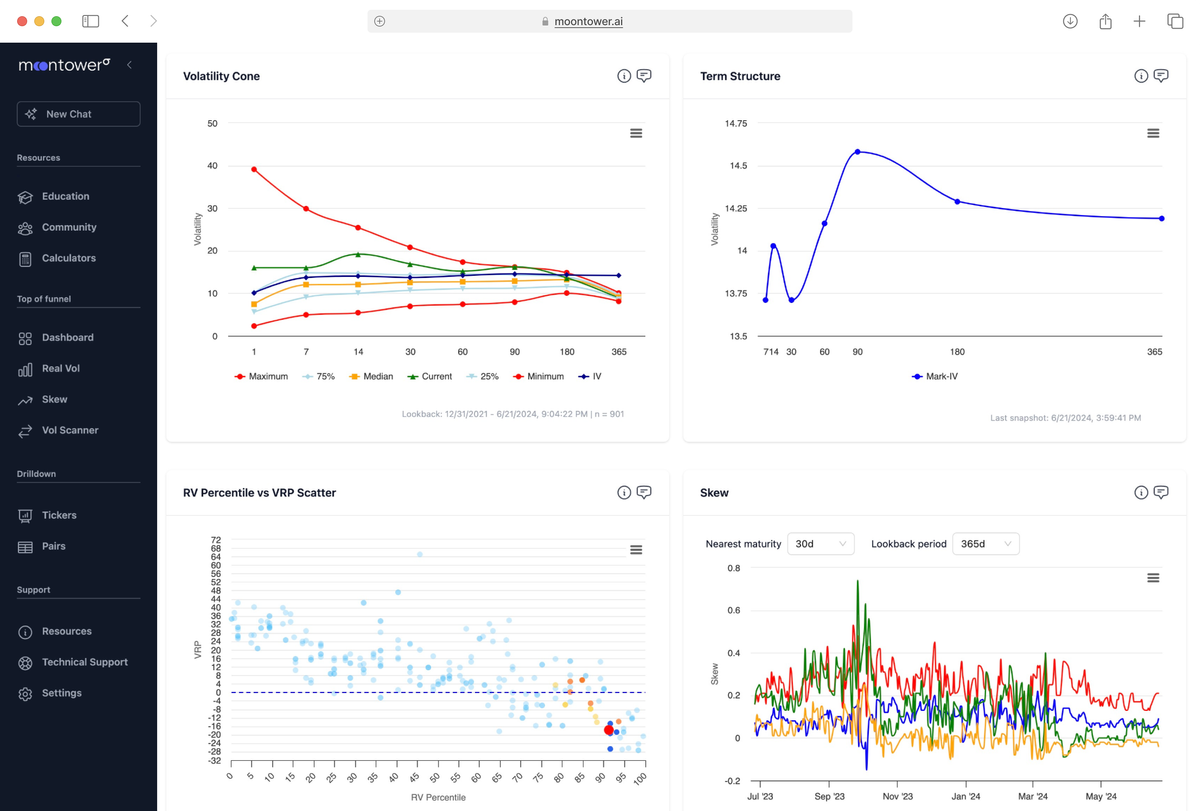
one-touch
probability vs delta
2 weeks ago I shared this tweet:
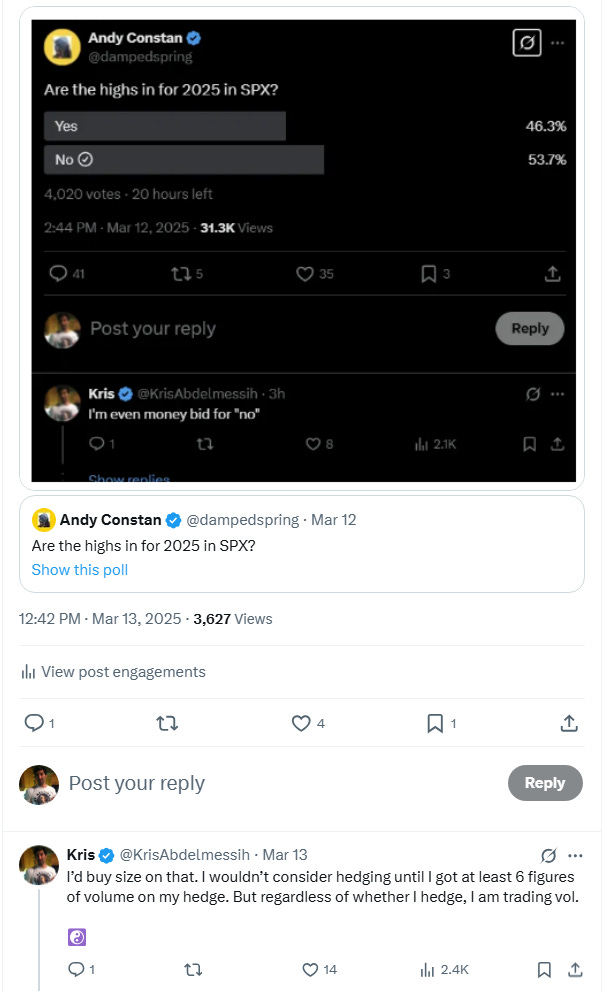
By saying I’d buy that proposition I’m saying “I’d buy that vol”
Andy, responded with a joke about what’s the “one touch” option worth, which I asked him to delete because I really would have liked a fool to sell me that proposition and Andy’s comment gives away the sauce.
[X’s killer app would be to escrow bets, but that’s another convo altogether]
I’d be a size buyer of a 50% probability that we get back to the highs before the end of the year.
It’s not bullishness. It’s vol trading. If you could buy that probability for 50% you could arb it vs the value of a one-touch call that pays off “if the stock ever touches or exceeds the strike price before expiry’.
That call will trade for a higher implied probability than 50%.
I’ve alluded to the rule of thumb before, but a one-touch probability is approximately twice the delta. At the time Andy tweeted, the highs would have corresponded to the 10% out-of-the-money call strike.
If we double the delta of that call, we estimate the one touch probability. Given SPX vol, I knew immediately that a 10% OTM call expiring on Dec 31 has a higher delta than 25% so the one-touch probability would certainly be at least 50% bid.
So as a matter of education there’s multiple lessons in this simple exchange.
Estimating the one-touch probability
Using our rule of thumb, we just need to estimate the delta.
@quantian’s got that trader reflex — do the napkin math:
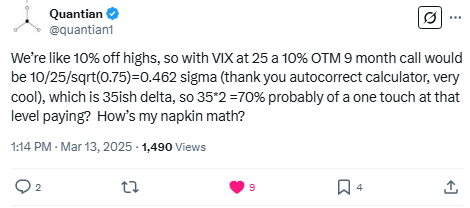
What did he do in steps:
- Used VIX as a proxy for implied vol which is annualized
- Scaled it to 9 months using √time or √.75… 25% * √.75 ~21.7%
- 10% / 21.7% ~ .46 sigma
- 1- normdist(.46) ~ .35 probability [assumes probability ~ delta]
- Double the probability —> 70% chance of one-touch
😈Possible enhancements to the estimate if you are a masochist:
With VIX at 25 I’d expect the term structure to be inverted so 9 month vol is lower. This would lead you to be more conservative on your delta. Sigma is directly proportional to our vol estimate so if we use 75% of the vol our sigma increases by 1/3 (since we dropped lowered the vol by 1/4). Normdist is not a linear function so still use the calculator and that pushes the delta down to .27 or 54% probability.The delta depends on the the moneyness of the forward price not the spot price and since interest is greater than dividends for SPY the delta is a touch higher.We’ll assume the positive skew embedded in Black-Scholes lognormality assumption offsets negative call skew. In sum I’d sell quantian’s delta of .35 and buy a delta of .27 so let’s call the fair delta .31 and the probability of the one-touch as 62%. I love getting even money odds when I should be laying 5-3.
Someone else knows their options btw:
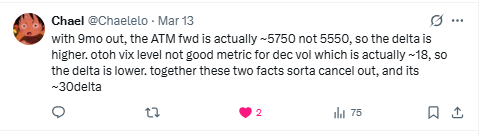
My response to quantian showed another way to conservatively estimate that the probability was higher than 50%

Intuition for why one-touch probability is 2x the probability of expiring ITM
I’ve discussed the shortcut before in crossing over zero. But I sketched an intuitive example using a trader’s favorite binkie — the binomial tree.
The image is self-contained explanation and follows from a simple assumption of a stock 50/50 to go up or down $1.
Starting from $100 and traveling 5 periods what’s the probability of the stock expiring $99 vs the probability of it “touching” less than $99?

Learn more:
Estimating the probability of a stock expiring above or below a strike from the delta works for relatively low vol or short dated option. The below post explains the real meaning of delta and why/how that estimate can break down.