Moontower Binomial Tree Explainer

Last week, in American options are not vanilla, we covered not only the concept of early exercise for American options, but rules for “optimal” early exercise.

If you want this broken down in video form, I direct you to Sheldon Natenberg’s explainer in CBOE’s educational series:

📽️ Early Exercise of American Options (CBOE, video lesson)

Today we’ll not only get into the common model used to price American-style options (you can use them for European-style as well, while Black-Scholes only works for European), but you can get hands-on to see how they work.

Just to tie a bow on last week’s post and not give you a false impression that early-exercise rules are dry calculations, here’s a shower thought I had laid out in a progression:

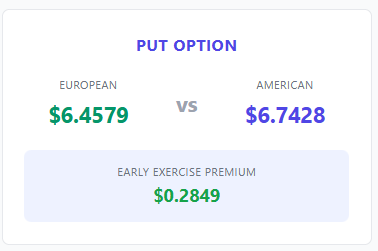
1. American reversal/conversion values are lower than European R/C because of early exercise. Basically, the expected value of T is smaller than T itself. “DTE” in the world of American-style options is not deterministic.
2. The spread between the Euro vs American R/C is a function of interest rate volatility. But I’ve never seen the spread directly modeled because the R in option models is taken as constant and “managed” at the level of portfolio Greeks [and general judgement].
3. I heard a few years ago a big MM took a hickey on early exercise mispricing during the 2022 rate hikes. That feels like a clue. I’m guessing they overvalued calls/undervalued puts because their R/Cs turned out to be too high. Amercian R/C values turned out to be much lower than the Euro values as they were assigned. In other words, the spread, which represents the value of the option to exercise early, was greater than expected.
4. I don’t know the details of what happened at that MM but I’m just guessing. If anyone wants to enlighten me you know how to reach me. I’m purely curious.
5. If this didn’t make sense, but you want it to, you like to be nerdsniped, which I appreciate. But this is definitely not something to be practically concerned about.

Before we go on to the tree models, how's this for an oblique, albeit grim, option play via 

Darkfire Capital LLC:

The survivor option:

Ok, here’s your free money of the day tweet - on your deathbed, instruct the trustee of your trust to buy as many brokered CD’s with the lowest coupon/longest maturities possible.

Once the death certificate is issued, forward it to broker and have them exercise the survivor’s option - bang, that CD priced at 88 is now par.

Laugh heartily from your coffin.

Tree models

Natenburg tells us that tree models are easier to grasp than Black–Scholes and can price both European and American options. He explains that the Cox–Ross–Rubinstein (CRR) binomial model remains one of the most popular implementations of trees to this day.

They work by pricing options just before expiry then working backward to today. At each node you ask: exercise now or wait?

Another SIG bootcamp exercise was to build these in Excel from scratch.

I used an LLM to help me code up both a tutorial and simulator so you can learn this stuff without signing a non-compete :-)

Step 1: Build the Stock Price Tree (forward in time)

💡CRR Parameters — where they come from

I’ve written a step-by-step explainer of the risk-neutral probability formula if you want to build up from intuition to math:

📐The General Formula to Back Out The Risk-Neutral Probability (moontower)

Step 2: Backward induction (the magic)

For European options, you skip the max with intrinsic (no early exercise), using only the Hold value.

A word on convergence

The binomial tree is a discrete way to approximate continuous price movements. As you increase the number of steps:

• Each time slice gets smaller.
• The tree gains more branches, resembling a smooth diffusion.
• The option price converges toward the “true” theoretical value.

Claude’s “rule of thumb” shows diminishing returns since you’re doing roughly 10× more computation for that extra 0.9% improvement:

• 100 steps ≈ 99% accuracy
• 1,000 steps ≈ 99.9% accuracy

Get your hands dirty

🌲Moontower Cox-Rubinstein Binomial Tree Lab: A self-explanatory demo

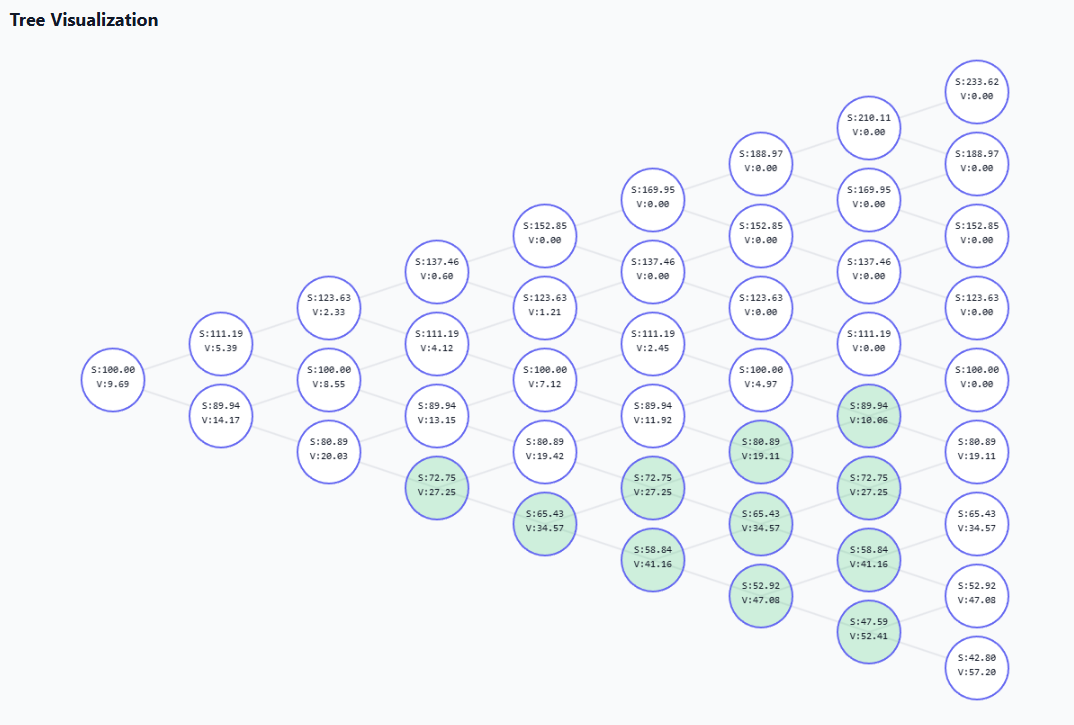
The green nodes represent early-exercise candidate conditions. A nice way to explore the tool is to see where the clustering occurs based on the inputs to build your understanding of what makes an option more or less likely to be exercised early.

🖥️Black-Scholes and Cox-Rubinstein side-by-side calculator