Intro to Simulating Dynamically Hedged Option Positions
daily delta hedging explained
Introduction to Dynamically Hedged Option Positions explains what a derivatives trader does and even more specifically a volatility trader.
In a sentence:
Most investors look for mispriced underlying securities and assume the options are “fair” while volatility traders look for mispriced options and assume the underlying is fair.
The moontower.ai application hands you vol trader goggles so you parse option decisions better. Most option users have a directional view already. Their source of edge is “upstream” of the options expression. The vol trader lens is a funnel to help you decide if options make sense for your directional/timing thesis (and if so what part of the surface). With practice you will be able to narrate if and why options were the right implementation. [I tried to suppress my meat-head accent to explain all this in my interview with Corey Hoffstein]
However, if you are in the much smaller set of traders who start with a volatility thesis, you are in the realm of “vol trading”. If you are vol trading, you want to isolate the mispriced volatility by hedging the directional risks (the option’s delta) lest they swamp your source of edge.
Do I advocate for viewers at home to become “vol traders”? Groan. I don’t even recommend college students pursue a life in vol trading. But preaching celibacy is a classic example of a “triumph of hope over experience”. So in the spirit of the Zelda shopkeeper…It's dangerous to go alone! Take this.
Today, new warrior, you get a wooden sword. It won’t slay the advanced bosses but it’s a massive leap from having the words “delta neutral” wash over you with zero context and the illusion of understanding.
This post is really a document with things to take from it.
It uses simulations to provide intuition for how realized volatility drives the p/l of delta-hedged position when hedging is done on a regular but discrete interval.
It answers questions of the variety:
“If I buy an ATM option for 20% and the stock realizes 25% what does my p/l look like?”
It includes:
- code
- plenty of pictures
- lots of explanations (sometimes scraping more advanced topics)
It’s appropriate for the vol-curious, aspiring traders, and professional trainees.
Senior traders will find thoughts they already have articulated in a different or useful way. A lot of practitioners tell me the writing gives them another way to communicate concepts they try to teach their assistants (that’s if they don’t just tell the trainees to read it and grok by the next day).
That’s my pitch.
Let’s hit it.
We are going to simulate, step-through, and summarize sets of delta-hedged option position scenarios.
The document does not lend itself to be fully published on Substack. Too many pictures and nesting modules for legibility.
Instead this post is an outline of the document. You can skip it and jump straight into the document.
This is the actual document:
🛣️Simulating Dynamically Hedged Option Positions
Outline
⌨️Setting up the simulation
- Simulate the daily logreturns of the stock
The returns are a function of expected return (in the case of B-S, it’s the risk-free-rate) and volatility.
🔀The underlying stock diffusion formula including explanation & code - Stepping through the strategy
Basics
Day 1
Buy the 1-year ATM call at its theoretical value priced with 25% volatility and hedge by shorting the stock in accordance with the option delta (.55).
Daily- Seed a realized vol that will transpire during the 1 year holding period. Each day will draw a random return centered around that realized volatility
- The implied vol of the option of 25% will not change
- Run batches of 500 simulations each. Each run in the batch will be seeded with the same realized vol. Some of the realized vols will be less than 25% and some will be greater than 25%.
Batches:
RV: 10%
RV: 20%
RV: 25%
RV: 26%
RV: 27%
RV: 30%
RV: 40% - Reprice the option with 1 day less to expiration
- Record share and option P/L based on that day’s opening position and the change in stock price
- Note: The simulation assumes the IV on the strike remains constant at 25%!
- Adjust the hedge by selling more stock or buying some back to remain neutral to the option’s new delta
Price a European-style option & compute Greeks

📐Equations for Black Scholes & Greeks (code)
📊Results
I. Zooming in on individual years
We will step through the case where buy the 1 year ATM call for 25% vol, and simulate a stock path that realizes an expected vol of 25%.
💡Sampling
Because our daily moves are sampled from a distribution with a 25% realized vol, the actual realized vol for any single run will differ from exactly 25%. The average realized vol over all 500 runs of 250 days in the batch is of course 25% even though any particular 1-year sim differs slightly.
Exposition
- We will step through several charts with explanations and interpretations for a single run randomly chosen from the batch of 500 runs seeded with a 25% realized vol.
- That template will help you step through other examples in the chartbooks below on your own to get a feel of how p/l paths look for various realized vols. Remember, in every case in this entire document we are assuming the implied vol of the option is 25% at all times.
A Tour Through A Single Run
- The code
- The feeder tables
- Charts & Interpretations
- Histogram of daily returns
- Stock Path vs Cumulative P/L
- Gamma vs Moneyness
Chartbooks for other realized vol paths
⚙The same setup every time
Buy a 1-year ATM call for 25% implied volThis implies our daily breakeven move is 1.5%
Hedge the delta daily
📄Realized Vol: 10%
📄Realized Vol: 20%
📄Realized Vol: 25%
📄Realized Vol: 26%
📄Realized Vol: 27%
📄Realized Vol: 30%
📄Realized Vol: 40%
II. High level lessons
In this section, instead of zooming in a particular run we will look examine what happens in a batch in aggregate. The format will be:
- Description of notable stats
- Observations from charts
- Summary table to compare batches
Description of notable stats
Let’s explore the batch of runs for 25% realized volatility.
For the 500 runs:
- Mean realized volatility is 24.77% with a standard deviation of 1.09%
- Therefore the realized underperformed the IV on average by .23% or less than a quarter vol point.
- The average P/L as a percentage of the initial option price of $9.95 over the 500 runs is -.5%. This makes sense since the RV slightly underperformed the IV.
- The initial vega is $.396. You would expect to make about $.40 per option for every 1 vol point of outperformance. Since we lost -.5% of our premium on average we can convert this to the statement: We lost .12 vol points on average with a standard deviation of 1.38 vol points.
This forms the basis of a simple, handy chart.
Observations from charts
We can see how our P/L varies in vol points as a function of RV-IV in vol points.
- When
RV-IVis positive, the RV outperformed the 25% IV and vice versa
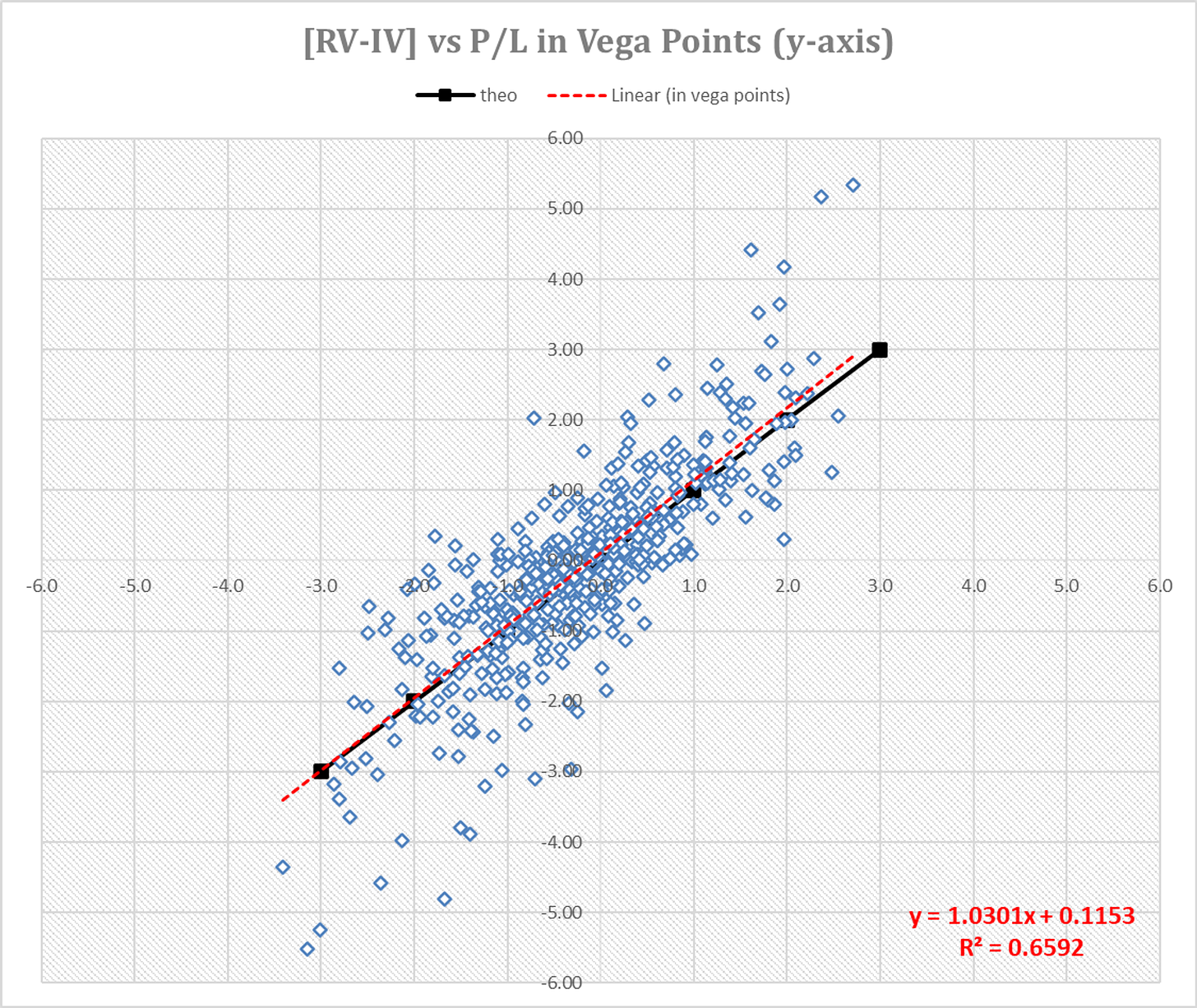
About the chart:
- The black line is a fabricated slope of 1 line. It’s a useful visual reference because it’s the line you’d get if your P/L in vol points simply comes down to “I win or lose vol points in direct proportion to the spread between RV and IV.”
- The red line is the regression line from the sample data. The R-square is for the red line.
Based on this batch of runs, it seems that when IV and RV are close together that the expected p/l in vol points will mirror the spread RV vs IV.
📊The results for all the runs
📄RV 10% batch (15 points underperformance)
📄RV 20% batch (5 points underperformance)
📄RV 26% batch (1 point outperformance)
📄RV 27% batch (2 points outperformance)
📄RV 30% batch (5 points outperformance)
📄RV 40% batch (15 points outperformance)
Summary table to compare batches
Note: Sharpe, P/L and Win% are from the perspective of the winning side (so if RV < IV it’s the seller’s POV)

Thoughts
- St dev of of RV-IV spread is larger if the RV is simply larger, but it’s close to a constant proportion of the RV level
- The goodness of fit between the P/L in vol points vs outperformance decays as RV and IV diverge
- Across the board, the standard deviation of the p/l in vol points is wider than the standard deviation of the RV-IV spread
- If you buy an option for about 5% less than what it’s worth (so if you bought 25% IV when the realized ended up being 26.25%), the Sharpe ratio would be about 1. In this example, the 1-year option priced with 25% vol is worth $9.95 so you would need to buy it for about $9.50 or a bit more than a vol point of edge to have a Sharpe 1 trade.
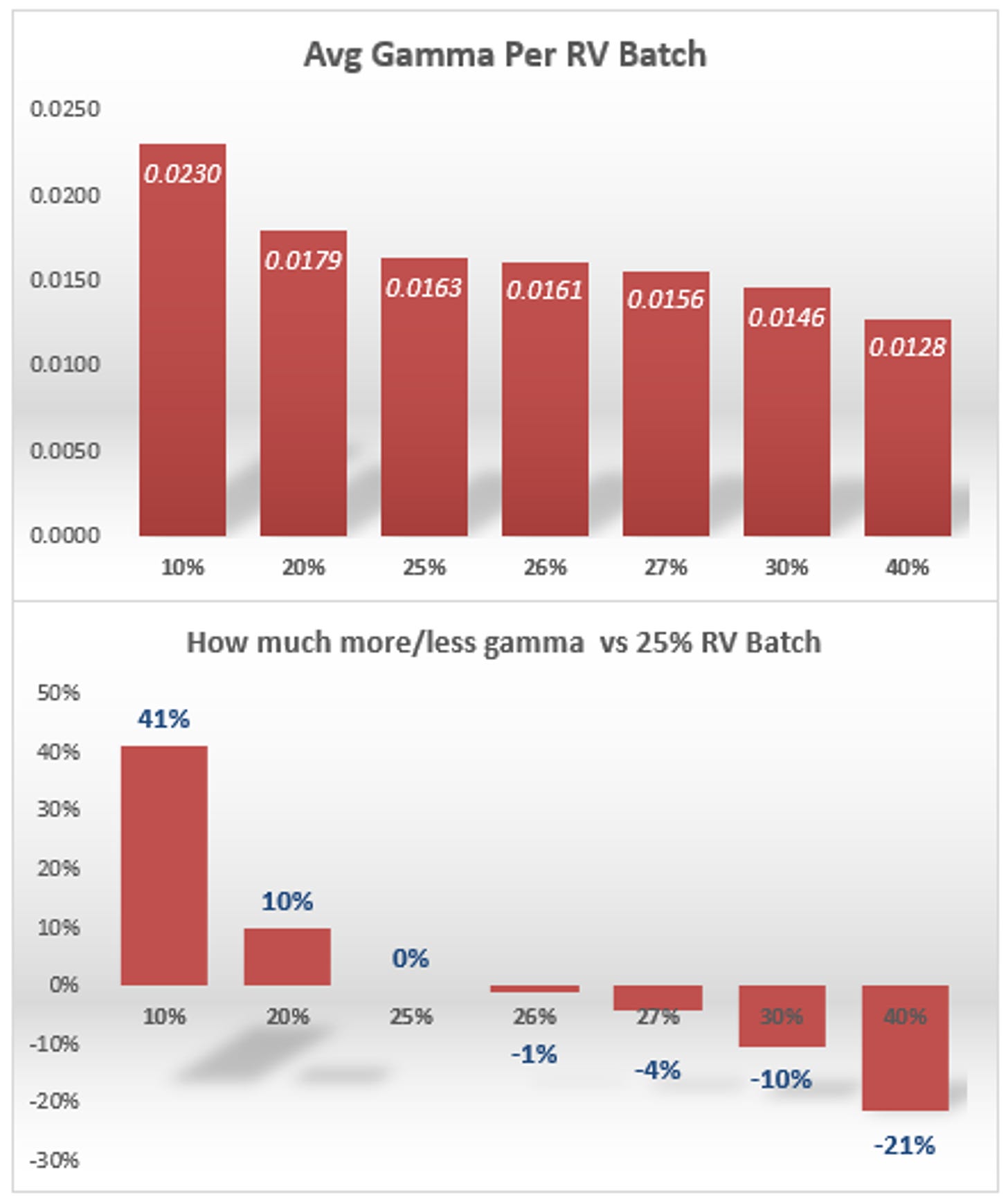
- The Sharpe of selling an option for 5 vol points of edge (25% IV vs 20% RV) vol seems to be about 50% higher than buying an option for 5 vol points of edge (25% IV vs 30% RV). I’m not sure what’s going on there but I’d hazard a guess based on a possible asymmetry — if the RV is very low, the stock probably doesn’t travel far so you maintain short gamma for a longer time as the stock stays nearer to the strike. Remember your hedged profits are a function of the daily over/underperformance of the implied move times the gamma. If you buy an option for much less than it’s RV, it’s possible that the high RV is generated by a large move that takes you far from the strike but then you are left without any gamma to scalp over the remaining option life. The results are congruent with this guess — the higher the realized vol, the less average gamma you have.
🚧Real World Caveat
If the realized vol is high, the implied vol will tend to follow it. For OTM options, the higher IV will narrow the distance between the spot and strike in standard deviations. This will “push” the option close to ATM, thus increasing its gamma.
There’s no advice here. It’s just a reminder that you need to think dynamically about how the greeks would change, in turn, altering your hedge ratios as your gamma and delta change.
When you mark IVs to market, you surrender control of your hedge ratios.If you mark your IV to model, you are ignoring any wisdom-of-crowds IV information from the surface.
You just have to understand the trade-offs and how the biases of each method interact with your particular strategy.
💡Concluding thoughts
This exercise used many assumptions. Some of them are quite benign in a real-world setting. For example, we assumed a constant RFR. But if you are an options trader who gets hosed by rho risk swamping your book, you have bigger issues.
There are 3 assumptions embedded in this work that should dominate your thinking as you translate the lessons to reality.
- IV is not constant.
Even if you don’t care about mark-to-market because you are dead-set on scalping the option to expiry and letting RV play out…the IV determines the delta, gamma, and theta. There is a terrific discussion in Financial Hacking about the biases of hedging on IVs that are both above or below the volatility that is eventually realized. - Brownian motion is not reality.
Real-world stock distributions differ from the assumptions of Black-Scholes. A lognormally distributed asset is a favorite to go down in price but has positive skew. This is the opposite of empirical observations in many markets! Option skews created butterfly prices which imply distributions that should match the real-world better (and if they didn’t do a fairly good job of that there would be easy alpha everywhere). All of the stats generated in these simulations are downstream of a Brownian motion diffusion process. - Costs are real.
The cost to hedge. The funding spread between your long and short rates on stock. The cost to trade the options themselves. In these simulations a 1-year option needs to be mispriced by 5% (ie you make $.50 edge on a $10 option) to have a 1 Sharpe ratio trade assuming NO TRADING OR FUNDING SPREADS.
Despite these deficiencies in the analysis, there’s a lot of basic intuition for delta-neutral vol trading buried within.
As a matter of personal taste, I think the most useful revelation is in the appreciation of path and its focal question: Did the moves that diverged from implied happen when my gamma was big or small?
The noise in vanilla options trading in many ways make it more complex than variance swaps which were invented to smooth the gamma profile of a vol position over both price range and time. The irreducible problem with variance swaps is their liquidity providers, in replicating the swap payoffs, cannot themselves escape the path dependence of their more liquid building blocks.
🚀Coming soon…
We will ship the monte carlo simulator used to generate these studies on moontower.ai so you can explore the paths of hedged option positions for various expiries, strikes, and vol levels yourself!
