I Felt Bad For Picking My 3rd Grader Off

In trading, “picking someone off” means trading against a counterparty who would flake on the price they offered you if they knew what you know.

If I lift an offer on a TSLA March call option because I’m bullish, the market-maker on the other side of my trade doesn’t care. They would still sell me the call even if I texted them my rationale. But if I had the divine knowledge that Elon was going to tweet in the next 10 seconds that earnings would be reported in March not February, then I would be knowingly “picking off” the market-maker. As an options trader, you need to defend against pick-offs. You also want alerts if someone else is making a price that is not incorporating material, public info. For example, if an OPEC meeting date was moved there might be a tiny window when you could disguise a calendar spread as a routine roll when really you are trying to pick off the other side before they get the memo.

[In reality, when such news happens, market-makers will “sweep” all the resting customer orders with price limits below or above the option’s new fair value. It’s very difficult to pick off another professional who is consuming a real-time news feed.]

A few categories of pick-offs:

• Pickoff trades related to changes in dates.
  
  If earnings are moved from early Feb to early March, then the “earnings volatility” needs to come out of the Feb expiry since you are no longer exposed to it, and the March options which now contain that volatility must appreciate relatively.
  
• Pickoffs related to change in carry
  
  If a stock announces a change in its dividend that will affect the carry embedded in the options. If a dividend is slashed, the calls go up relative to the puts. Market makers need to be on top of how corporate actions affect the inputs into their pricing models.
  
• Pickoffs related to changes in baskets
  
  If an ETF’s constituents change that affects vol of the underlying basket. If an ETF restricts creations, this can lead to the options and ETF becoming mispriced (one day I’ll tell the story of how this personally cost me 6 figures).

Pickoffs In Real Life

The tradition of trading floors is full of insane prop betting stories (NYMEX vets have so many to choose from but my personal favorite was watching one guy successfully pound 20 Coors Lites in an hour in one of the upstairs offices).

But picking people off can be as easy as making bets with folks who are arithmetically challenged. Most people are. You only need to look up polls by @10kdiver to see that even professional investors, a subset of the population who should be able to compute a return, struggle numerically.

I am overstating the case a bit.

1. I don’t know how many of those respondents are professional investors. I’d also admit there are times I’m impatient and just take a guess just to see the results. This is probably common behavior.
2. When confronted with a bet, people’s defenses go up. They are wary of strangers bearing gifts and will assume there’s a catch.

Now that was a long-winded, but hopefully fun, introduction to a story that I will improve your numerical intuition and illuminate a lesson that is central to both investing and engineering problems.

The Proposition

My 3rd-grader came home with a packet of math worksheets from school. Two of the sheets, a total of 10 questions, were incomplete. He said the teacher didn’t require those sheets to be done.

What a bummer.

I thought they were the best questions from the whole packet. I asked him to solve the total of 10 questions but decided to make my request a little spicier. I offered him the following bet:

If you get them all correct, I will give you $5. Otherwise, you owe me $5.

He thought for a moment, then accepted. Before he went off to work on them, I started to wonder if my impulsive proposition was fair.

Is It A Fair Bet?

After eyeballing the questions, I estimated he had a 90% chance of getting any question correct. Another way to say that, is I expect he gets 1 wrong on average. Right off the bat,  I think I’m going to win. It’s not a fair bet.

This led me to compute a couple numbers.

1. If my estimate of 90% hit rate per question is correct, what’s the chance he gets them all correct?
   
   .90¹⁰ = 35%
   
   That means he’s almost a 2-1 underdog
   
2. What would his hit rate need to be per question to make the bet fair?
   
   First we need to convert what a fair bet means in math language. This is straightforward. Since it’s an even $5 bet then the fair proposition would not be, on average, he gets 1 wrong, but that he gets all the questions correct 50% of the time. 
   
   x¹⁰ = 50%
   
   x = .50 ^ (1/10)
   
   x = 93.3%
   
   So if he had a 93.3% chance of getting any single question correct, then he has a 50% chance of winning the bet.

Flipping The Odds In His Favor

I’m not trying to take candy from a 3rd grader, I just wanted to make him more eager to do the questions. So, I tweaked the bet after he returned with the answers. Each of the 2 worksheets had 5 questions each. I decided to batch the bet as follows:

If he gets all the questions correct, he wins.

If he gets all the questions in one batch correct but not the other, it’s a push.

If he gets less than 100% on each batch then he loses the bet. 

How did this tweak alter the proposition?

In the first bet, if he got anything wrong, he lost. With these rules, he only loses if he gets, at least, one wrong in each batch.

We need to analyze all the possible outcomes that can occur with 2 batches.

First, we must ask:

What is the probability he gets all the questions right within a batch of 5 questions?

Assume he has a 90% hit rate again. 

.9⁵ = 59%

So for either batch he has a 59% chance of getting a perfect score and a 41% chance of getting at least one wrong (ie a non-perfect score). 

Now we must consider all the possible outcomes of the proposition and their probabilities.

1. Perfect score in both batches
   
   59% x 59% = 34.8%
   
2. Perfect score in one batch but not the other
   
   59% x 41% = 24.2%
   
3. At least one wrong in both batches
   
   41% x 41% = 16.8%

If we sum them all up we get 75.8%.

Wait, these don’t add to 100%, what gives??

We need to weigh these outcomes by the number of ways they can happen.

The possibilities with their probabilities are as follows:

• Win, Win = 34.8%
• Win, Lose = 24.2%
• Lose, Win = 24.2%
• Lose, Lose = 16.8%

Collapsing the individual possibilities into the proposition’s probabilities we get:

• Win: 34.8%
• Push: 48.4% (24.2% + 24.2%)
• Lose: 16.8%

These probabilities sum to 100% and tell us:

1. The most likely scenario of the bet is a push, no money exchanged
2. Otherwise, he wins the bet 2x more than he loses the bet

This is a powerful result. Remember, his hit rate on any individual question was still 90%. By batching, we changed the proposition into a bad bet for him, into a good bet because he gets to diversify or quarantine the risk of a wrong answer.

Even More Diversification

With 2 batches we saw the range of possibilties conforms to the binomial distribution for n = 2:

p² + 2p(1-p) + (1-p)²

where p = probability of perfect score on a batch

In English, the coefficients: 1 way to win both + 2 ways to push + 1 way to lose both

What if we split the proposition into 5 batches of 2 questions each?

These are the bet scenarios:

1. Win =  5 pairs of questions correct
2. Lose = at least one wrong in each of the 5 pairs to lose the bet
3. Push = and any other combination (i.e. 3 perfect batches + 2 imperfect batches)

How do the batch outcomes roll up to the 3 bet scenarios?

1. We must count how many ways there are to generate each of the scenarios.
2. We must probability weight each way.

The summary table shows the work.

[Note the coefficients correspond to the coefficients for the binomial expansion (x+y)^5 which is also the row of Pascal’s Triangle for N = 5]

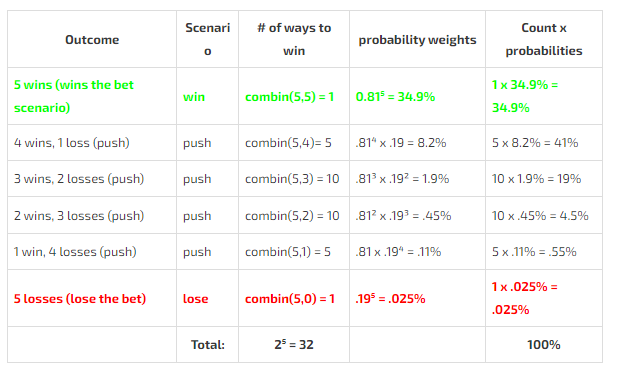
The net result of quarantining the questions into 5 groups of 2:

35% chance he wins the bet

65% chance he pushes on the bet

Nearly 0% chance he loses on the bet!

If you took this quarantining logic further and treated each question as its own bath then the new phrasing of the bet would be:

If he gets every question correct, he wins

If he gets every question incorrect, he loses

Any other scenario is a push

The corresponding probabilities:

Win = .9¹⁰ = 35%

Lose = .1¹⁰ or ~0%

So the benefits of separating the bets were mostly achieved above when we batched into groups 5 pairs of questions.

Conclusion

The first required my son to get a string of questions correct. Even though I estimated he had a 90% chance of getting any question correct, by making the net outcome dependent on each chain-link the odds of his success became highly contingent on the length of the chain.

With a chain length of 10, the bet was unfair to him. By changing the bet to be the result of success on smaller chains (the batches) I changed the distribution of outcome. It did not increase his chance of winning, but it reduced his chance of losing by creating offsetting scenarios or “pushes”. In other words, the smaller chains reduced his overall risk without sacrificing his odds of winning. It was a free lunch for him.

When you create long chains of dependency (ahem, positive correlations), an impurity in any link threatens your entire proposition. In these examples, we are dealing with binary outcomes. This is a trivial analysis. With investing, the distributions of the bets are not easily known.  It is well-known, however, that diversifying or not putting all your eggs in one basket is a free lunch. Still, if the investments are highly correlated, you may be fooling yourself and depending on a long chain.

Imagine if the 10 questions my son had were the type of word problem where the answer to each question is the input to the next. That’s a portfolio of highly correlated assets. If you are “yield-farming” crypto stablecoins you have probably thought about this problem. Spreading the risk across many coins can offset many idiosyncratic risks to the protocols. But is there a translucent, hard-to-see chain of correlation tying them all together that only reveals itself when the whole background goes black? That’s systemic risk. Ultimately, the only hedge to such a risk is position sizing at the aggregate level where you sum the gross positions. This is why stress-testing a portfolio to that standard is a quant’s “last level of defense”.

Jarvis, what happens to my portfolio when all correlations go to one?

[If you are in the investing world you will see parallels to this lesson in the ergodicity¹ problem.]

Oh yea, how’d the bet with my 3rd grader go?

He got a perfect score on one batch of 5, and he got 1 wrong in the second batch. So the overall bet was a push, and his old man didn’t do so bad in estimating he’d have a 90% hit rate.