Connecting Vol Surfaces To Option P/L

The small cap leg of the rotation in mid-July 2024 can be seen in IWM.

I cherry-picked points before the move and at a peak.

In 4 business days, July 10th to July 16th, IWM rallied >10%

The vol surface for the 6-month option expiry (Jan 2025) had a near parallel shift higher.

That’s a substantial move in a 6-month surface but considering ATM vol was 18.8% before the move, a 10% rally in 4 trading days is 4 standard deviation event. Some breathlessness in the surface seems reasonable.

💡To compute how far that move is plug and chug into this equation:

In this post, we will use these vol curves to compute returns on various options. We’ll use a mix of socratic method and simply making observations to get you in comfortable. This is a set-up for upcoming posts that will go deeper into dynamically hedged option p/ls and option p/l attribution.

We don’t have to go into anything more than arithmetic to cover a lot of ground and understanding.

The pre-work for this post was to use a European-style option calculator with these vol surfaces and assume 0 RFR and divs. These simplifications have no material impact on the intuition we’re building.

Sample of what this looks like on 7/10/24 with the IWM surface snapshotted with the stock at $202.97

We will focus on:

• ~.75d call (.25d put)
• ATM call (~.53d — do you remember why ATM options have deltas > .50?)
• ~.25d call

Outright directional trades

Imagine 3 scenarios where you are bullish and buy calls on 7/10. In each scenario you choose a different option. Because of the giant rally in the next 4 days you are going to win on the delta, gamma, and expansion in IV. Remember the surface change:

Observations:

• You make the most money per contract on the .76d call because it has the highest delta and the stock rallied >$21
• You make the highest return on the lower delta options. If you were going to invest a fixed number of dollars (say $100k), you would have gotten the most bang for your buck with the 223 calls which had .25d on July 10th.

This is basic, directional option p/l stuff but never hurts to reinforce.

Let’s move on to delta-neutral trades.

Delta-neutral

Suppose we didn’t have a directional bias on IWM but we know that small-caps have been massively underperforming larger stocks. Maybe this feels somewhat unstable and we think there’s a large move coming. You envision 3 scenarios:

1. IWM has a giant catch-up rally
2. The performance spread will widen even further as IWM longs are really just bagholders with a mean-reversion addiction. You think their thesis is grounded in that keep them scaling into value-traps and the realization that they are the fish at the table will lead to abandonment and capitulation — ie IWM is hanging on by a thin string of hope. The 6 month options will give you time to an unexpected destabilizing move.
3. The large caps fall while IWM sputters around not doing much.

You rule out #3, but can’t decide between scenarios #1 and #2. In both of those scenarios, IWM making a large move is the driver of the spread narrowing. You’re going to buy vol delta-neutral (you will sterilize the delta of the option at the initiation of the trade).

Unable to muster a directional bias, you decide to randomly choose a strike to buy. Either the 25d put, the ATM call, or the 25d call. Call vs put doesn’t really matter because you will hedge so that your delta is zero anyway.

It’s late in the day Wednesday, July 10th. The stock is $202.97.

Since OTM options are tighter/more liquid than ITM options you focus on the:

• 185 put
• 203 call
• 223 call

You will buy 100 contracts of one of those options and delta hedge it.

☘️☘️☘️

What luck!

The day after you buy the option delta neutral the stock popped nearly $10 higher to $211.

But since it’s your birthday weekend, you left town and disconnected. You get back just in time for the close on Tuesday, July 16th.

The stock is up >10% since you went on vacation. It is $224.32!

You started delta-neutral, but considering how large the move was compared to the implied move in the options you expect to be up a lot of money on your portfolio of shares plus 100 contracts.

💡Useful rules of thumb

At 16% annualized vol:

• daily implied move = 1% (16%/ √251 OR 16%/~16)
• weekly implied move = 2.2% (16%/ √52 OR 16%/~7)
• monthly implied move = 4.6% (16% / √12 OR 16%/3.5)

We didn’t even need to compute that z-score earlier in the post to know that a 10% move in less than a week was substantial compared to what option premiums implied.

Here’s what happened on a fixed strike basis between the 2 vol surfaces from 7/10 to 7/16:

Things to notice and rotate in your brain:

• The vega, gamma, and theta are highest near the ATM strike
• The strike vols increased in a fairly uniform way
• When we are zoomed out we can easily say “this option trader has a long vol position”. But you’re p/l is a function to what happens to option premium. Talking about vol is useful because it’s how we reason about the relative cheapness or expensiveness of options…but when you get down to the actual inventory you hold in your account you want to be more granular. What happened to the strike vol of the option you actually own? In this example, because of the size of the rally, your long option position would make money even if the strike vol was down. You would have gotten paid on gamma — as the stock climbs, your call delta is getting longer (or your put delta is shrinking) while your physical share position is static. So your portfolio delta is increasing as the stock goes up! You can infer the significance of p/l attribution…your vega p/l could have been negative while your gamma p/l could have more than made up for it. In this case, your vega and gamma p/l’s would be positive. We aren’t going to do attribution today, but we are getting you loose 🙂

A skew detour

In Scatterplot Gallery I talk some about how skew flattens when vols expand to high levels and vice versa.

In this case, the strike vols rose fairly uniformly.

Imagine a vol curve summarized as:

25d put = 20% IV (33% skew relative to ATM)

ATM call or put = 15% IV

25d call = 12% IV (-20% skew relative to ATM)

Ok, let’s say all strike vols uniformly increase by 100 points.

Respectively:

120% IV

115% IV

112% IV

There’s basically no skew in this market.

(Experienced traders will recognize a sleight of hand —> If the vols go up by that much than on a fixed strike basis all of these options will tend towards .50d and we are no longer measuring 25d to 50d skew. We can’t look at the same strikes to measure skew as the vol changes because of the recursion of vol impact on delta…I know the word “vanna” typically is followed by “flows” but this is vanna in its platonic form. Change in delta per change in vol)

Even though I used a sleight of hand in the extreme example, it’s useful to make it memorable that skew flatten as vol ramps.

We can see this even in our IWM example. Above we looked at a fixed strike vol change. This is a floating strike vol change where we compare the vols at fixed deltas instead of strikes.

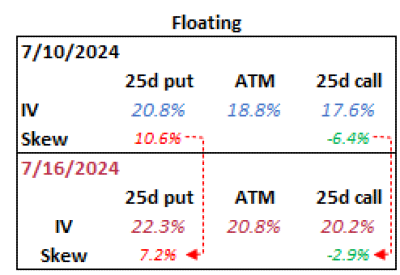
I hope the detour didn’t add confusion. I just wanted to show the “skew flattening” in the wild and it was a handy device for contrasting fixed strike vs floating strike changes.

[Sometimes these 2 ways of comparing vol changes are referred to as “sticky strike” vs “sticky delta”. Traders will often run models that assume the market locally behaves in one of these ways, but there are hybrid specifications as well. This is definitely in the weeds, so don’t stress out about it unless your income depends on it. If that is the case, stress hard, because this is the type of stuff that you split hairs over in practice.]

Let’s return to delta-neutral land.

What is the p/l for each of the 3 options we could have chosen to buy 100 contracts and then neutralize the delta for on 7/10/24?

I’ll provide summary tables which show the p/l as well as the required rebalance quantities you must trade to get back to:

1. delta neutral
2. your initial vega position (remember, you were definitely long vol, but because the spot price and IVs changed your vega position changed. Time also passed but this has an immaterial influence. We make the assumption that you will trade some amount of ATM options to get back to your initial vol length)

Scenario 1: You bought 100 lots of the 185 puts & hedged on a .24 delta

Notes:

• As your long put is now far OTM (it’s only -.11 delta now), you are not as long vega as you started. You are now only long $2,980 vega so you need to buy about 25 ATM options if you want to maintain the same vol length. Now that the big move occurred you’d need to re-assess your vol axe. Maybe you are happy the vol position is small. Maybe you want to flatten your vega entirely or even go short. The example just shows how even though the vol increased, the option’s moneyness is causing it to have less vega than it did before the move. (There’s a little rabbit hole in there because when vol increases, the vega of an OTM option also increases. In this case, the increase is swamped by the option being low enough delta that the net effect is less vega overall).
• Your long deltas because you owned 2,400 shares but your puts are only spitting off -1,100 deltas, so you must sell 1,300 shares to rebalance to delta-neutral.

Scenario 2: You bought 100 lots of the 203 calls & hedged on a .53 delta

Scenario 3: You bought 100 lots of the 223 calls & hedged on a .25 delta

The main observation for this scenario is your .25 delta call is now a .55 delta call and you are longer vega! You now get to sell options to get back to your original vol length. It’s a high class problem to have a growing supply of ammo as chaos sets in.

The strike vol went from 17.6% to 20.9% while the calls went from .25 delta to ATM and you are longer 25% more vega.

This is worth contrasting with Short Where She Lands, Long Where She Ain’t. In this 223 call example, the stock went to our long strike and we won big. The difference stems from 2 forces:

1. These options are not near expiry. They have plenty of vega in them and vol is roofing. These premiums are just getting bigger.
2. We got to the strike very fast. We almost gapped here. Because you stepped away for 4 days, you didn’t have a chance to sell the stock at $211, $213, and $217 to stay delta-neutral. By being negligent and opting for a tan, you let your long gamma ride a trend.

That’s a lot to think about for now but it will keep you limber when we get into option p/l attribution with delta hedging.